Commented examples
Simple example, one action, quantity fixed

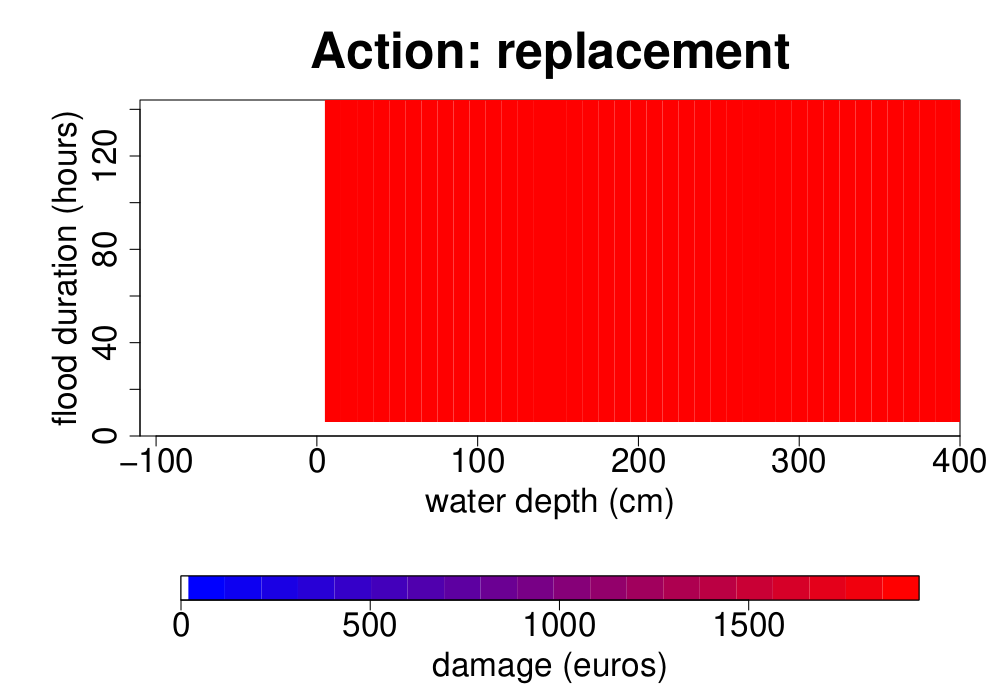
Figure 1 shows the elementary damage function of an air conditioner. If this elementary component is affected by a flood with a positive water depth and a positive water duration, it needs to be replaced. Hence, the damage is constant over all combinations of positive water depth and flood duration.
In this example, the values taken by the components of equation of the elementary damage section are the following:
- \(e\) refers to an air conditioner;
- \(S\) comprises 2 states:
- \(s_{1}\): normal state (no action needed);
- \(s_{2}\): destroyed (needs to be replaced);
- \(p_{s_{1}}(h, d)\) is equal to 1 if the water depth is negative or null or if the flood duration is null and to 0 otherwise;
- \(p_{s_{2}}(h, d)\) is equal to 1 if the water depth and flood duration are strictly positive and to 0 otherwise;
- \(i_{s_{1}}(h, d)\) and \(i_{s_{2}}(h, d)\) are always equal to 1;
- \(c_{a_{s_{1}}}\) is equal to 0 because no action needs to be done when the component is already in the normal state;
- \(c_{a_{s_{2}}}\) is equal to €1950;
- \(h_{a_{s_{1}}}\) and \(h_{a_{s_{2}}}\) are equal to the height of the air conditioner.
Example, several actions, quantity fixed
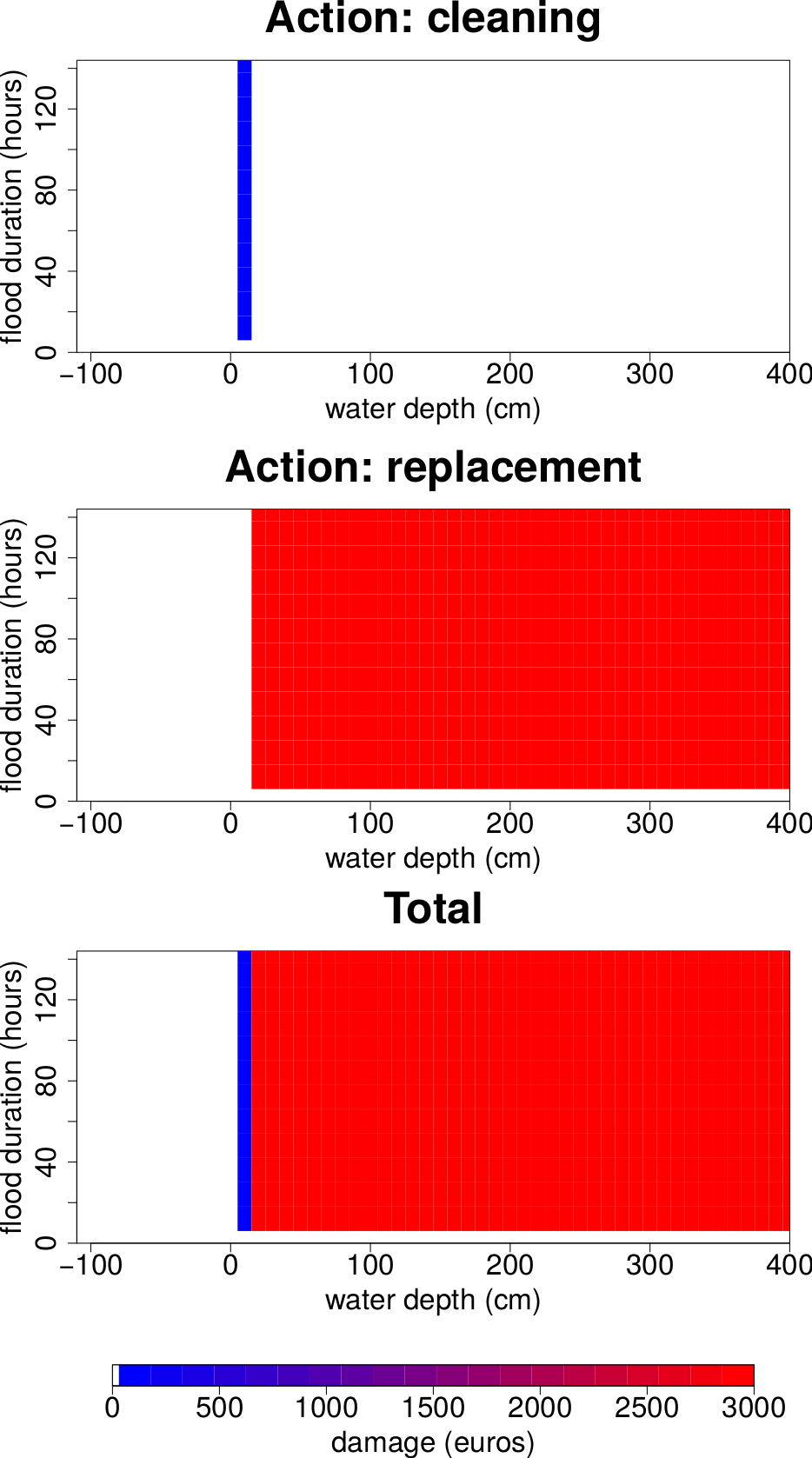
For some elementary components, different actions need to be performed depending on the flood parameters. For instance, figure Figure 2 shows the elementary damage function of a vending machine. It is the sum of the costs of two actions: cleaning and replacement. For all flood durations, if the vending machine is affected by a water depth between 0 and 19 cm, it must be cleaned. The cost of this action does not depend on the flood parameters. If the water depth is higher than 19 cm, the vending machine must be replaced. Again, the cost of this action does not depend on the flood parameters.
In this example, the values taken by the components of equation of the elementary damage section are the following:
- \(e\) refers to a vending machine;
- \(S\) comprises 3 states:
- \(s_{1}\): normal state (no action needed);
- \(s_{2}\): dirty state (needs to be cleaned);
- \(s_{3}\): destroyed (needs to be replaced);
- \(p_{s_{1}}(h, d)\) is equal to 1 if the water depth is negative or null or if the flood duration is null and to 0 otherwise;
- \(p_{s_{2}}(h, d)\) is equal to 1 if the flood duration is strictly positive and the water depth positive and below 20 cm and to 0 otherwise;
- \(p_{s_{3}}(h, d)\) is equal to 1 if the flood duration is strictly positive and the water depth higher than 20 cm and to 0 otherwise;
- \(i_{s_{1}}(h, d)\), \(i_{s_{2}}(h, d)\), \(i_{s_{3}}(h, d)\) are always equal to 1;
- \(c_{a_{s_{1}}}\) is equal to 0 because no action needs to be done when the component is already in the normal state;
- \(c_{a_{s_{2}}}\) is equal to €50;
- \(c_{a_{s_{3}}}\) is equal to €3000;
- \(h_{a_{s_{1}}}\), \(h_{a_{s_{2}}}\), and \(h_{a_{s_{3}}}\) are equal to the height of the vending machine.
Example, complex actions
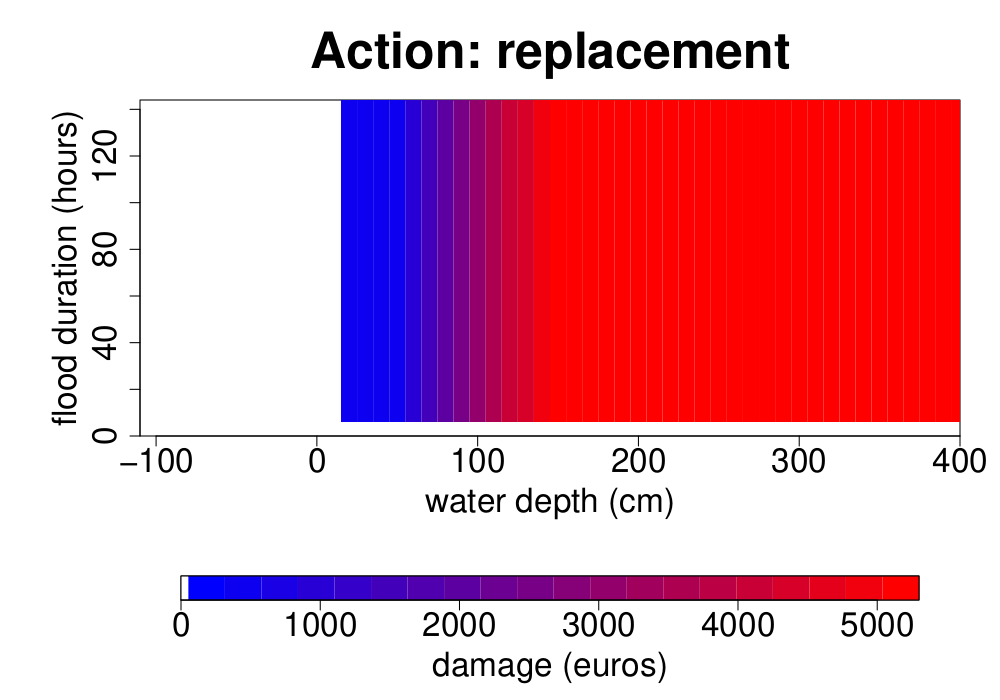
For some elementary components, the probability that an action has to be performed after a flood can be strictly positive but lower than 1 and depend on the flood parameters. For instance, figure Figure 3 shows the elementary damage function of a gas-operated boiler. For all flood positive flood durations and for water depths equal or higher than 20 cm, the probability that this elementary component has to be replaced is strictly positive:
- for water depths comprised between 20 cm and 100 cm, this probability is equal to 0.1;
- for water depths comprised between 100 cm and 150 cm, this probability is equal to 0.6;
- for water depths higher than 150 cm, this probability is equal to 1.
For a given combination of water depth and flood duration, the damage to a gas-operated boiler is equal to the replacement cost of this elementary component multiplied by the probability that the component has to be replaced.
In this example, the values taken by the components of equation of the elementary damage section are the following:
- \(e\) refers to a gas-operated boiler;
- \(S\) comprises 2 states:
- \(s_{1}\): normal state (no action needed);
- \(s_{2}\): destroyed (needs to be replaced);
- \(p_{s_{1}}(h, d)\) and \(p_{s_{2}}(h, d)\) are respectively equal to:
- 1 and 0 if the water depth is below 20 cm and the flood duration negative or null;
- 0.9 and 0.1 if the flood duration is strictly positive and the water depth between 20 cm and 100 cm;
- 0.4 and 0.6 if the flood duration is strictly positive and the water between 100 cm and 150 cm;
- 0 and 1 if the flood duration is strictly positive and the water depth higher than 150 cm;
- \(i_{s_{1}}(h, d)\) and \(i_{s_{2}}(h, d)\) are always equal to 1;
- \(c_{a_{s_{1}}}\) is equal to 0 because no action needs to be done when the component is already in the normal state;
- \(c_{a_{s_{2}}}\) is equal to €5300;
- \(h_{a_{s_{1}}}\) and \(h_{a_{s_{2}}}\) are equal to the height of the boiler.
Example, role of humidity
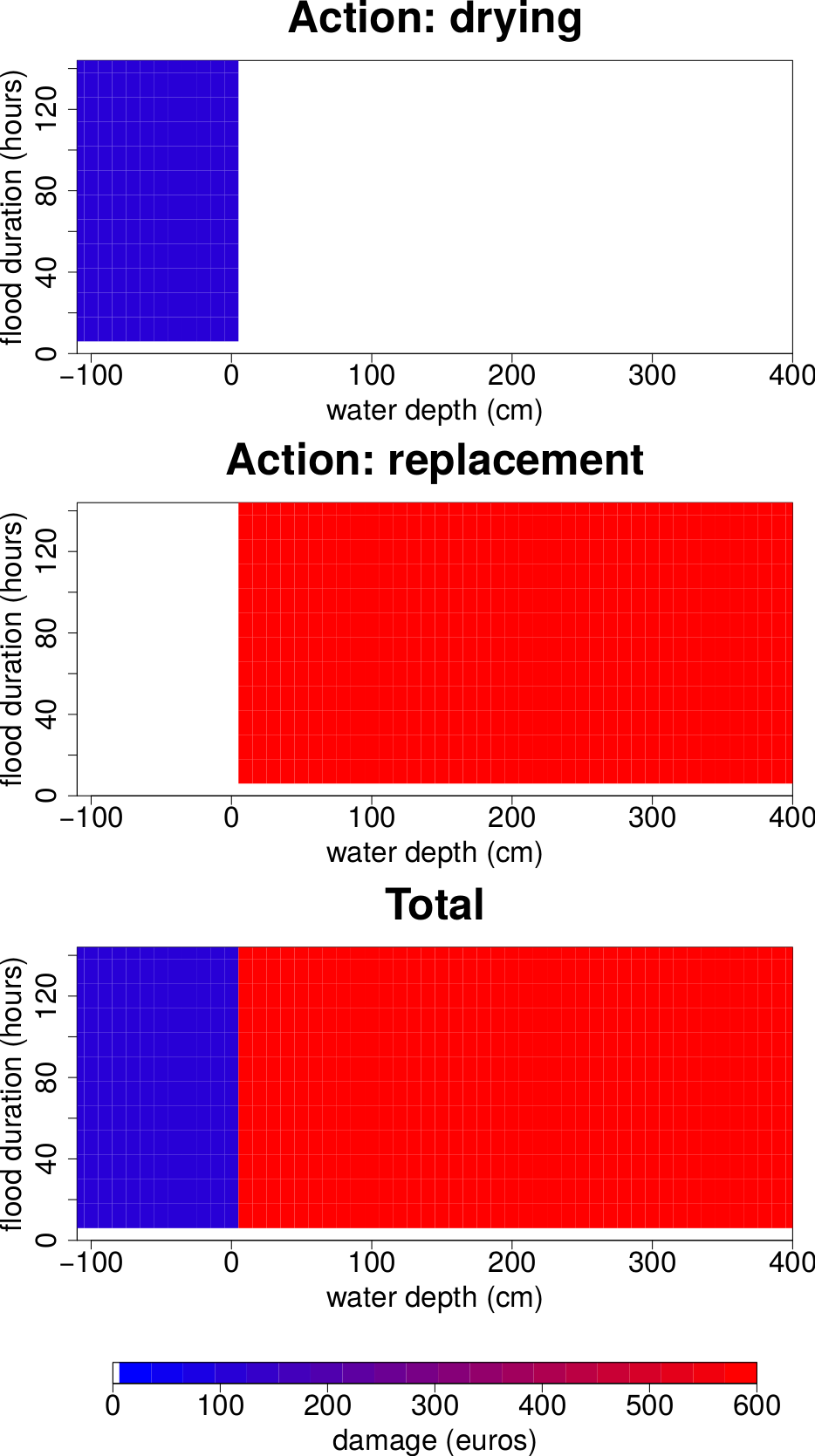
Some elementary components can be damaged by a flood, event if they are not immersed. That is the case for elementary components that are moisture-sensitive. For instance, Figure 4 shows the elementary damage function of a computer. If the room in which the computer is located is flooded, but the water does not reach the computer, the computer needs to be dried. That is why the damage is positive for negative water depths (relative to the computer). If the computer is immersed, it needs to be replaced.
In this example, the values taken by the components of equation of the elementary damage section are the following:
- \(e\) refers to a computer;
- \(S\) comprises 3 states:
- \(s_{1}\): normal (no action needed);
- \(s_{2}\): moist (needs to be dried);
- \(s_{3}\): destroyed (needs to be replaced);
- \(p_{s_{1}}(h, d)\) is equal to 1 the the flood duration is negative or null and to 0 otherwise;
- \(p_{s_{2}}(h, d)\) is equal to 1 if the water depth is negative and the flood duration strictly positive and to 0 otherwise;
- \(p_{s_{3}}(h, d)\) is equal to 1 if the water depth and the flood duration are strictly positive;
- \(i_{s_{1}}(h, d)\), \(i_{s_{2}}(h, d)\), and \(i_{s_{3}}(h, d)\) are always equal to 1;
- \(c_{a_{s_{1}}}\) is equal to 0;
- \(c_{a_{s_{2}}}\) is equal to €120;
- \(c_{a_{s_{3}}}\) is equal to €5300;
- \(h_{a_{s_{1}}}\), \(h_{a_{s_{2}}}\), and \(h_{a_{s_{3}}}\) are equal to the height of the computer.
Example, quantity to be fixed
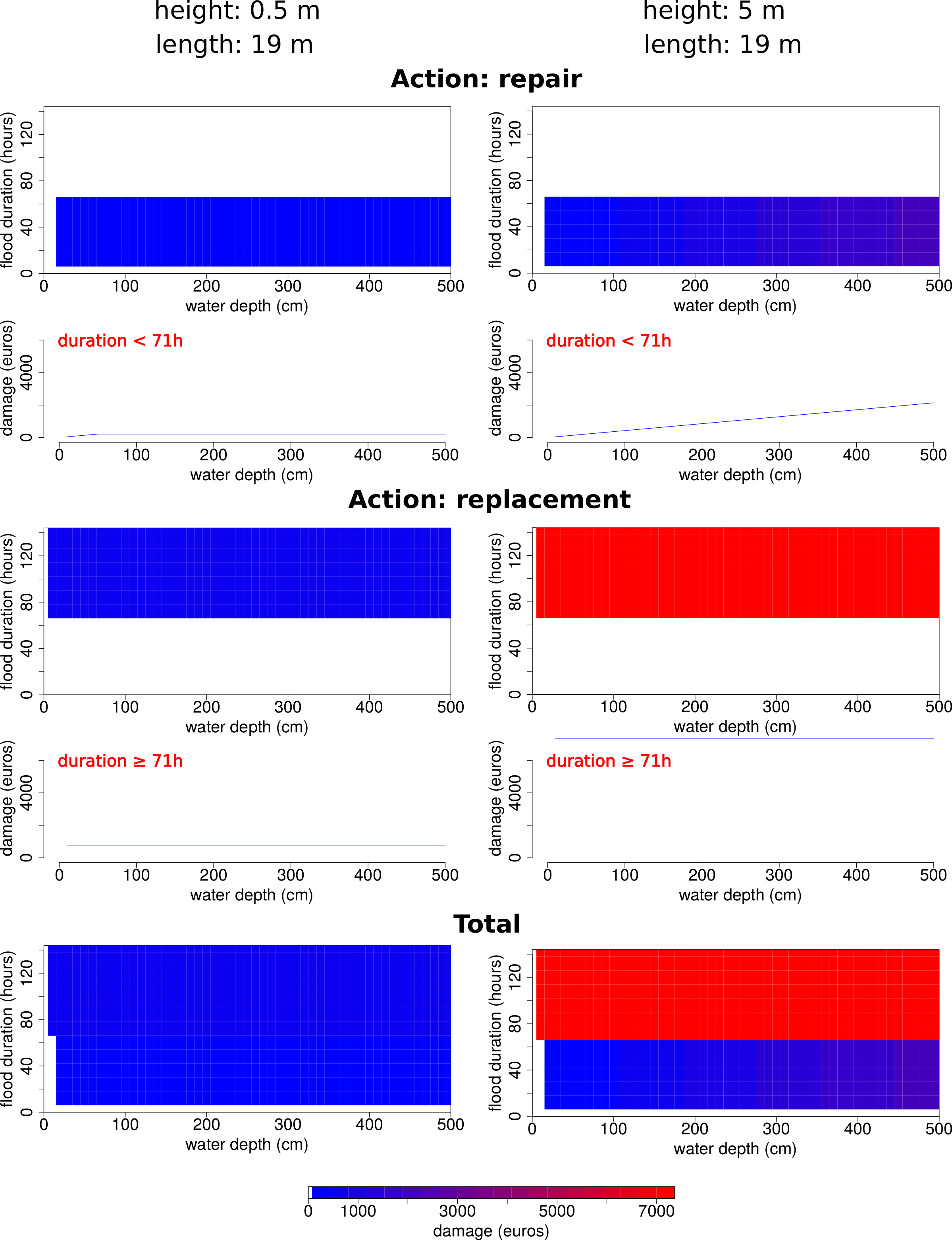
The damage functions of some elementary components depend on their geometry (e.g. the walls, the floors). Figure 5 shows the damage functions of 2 rectangular partition walls in masonry that have a length of 19 m but different heights: 1 has a height of 0.5 m and the other has a height of 5 m. Both walls need to be:
- repaired if they are affected by a flood that lasts less than 71 h;
- replaced if they are affected by a flood that lasts at least 71 h.
For flood durations below 71 h, only the portion of the wall that was in contact with water needs to be repaired. For flood durations of at least 71 h, the entire wall has to be replaced. Since the repair cost is proportional to the surface of the wall that needs to be repaired, it increases with the water depth up to the wall height. The replacement cost does not depend on the flood parameters but depends on the wall surface. As a result, for a given combination of flood duration and water depth, the damage that affects a wall increases with the wall surface.
In the example of the partition wall that has a length of 19 m and a height of 5 m, the values taken be the components of equation of the elementary damage section are the following
- \(e\) refers to a partition wall in masonry that has a length of 19 m and a height of 5 m;
- \(S\) comprises 3 states:
- \(s_{1}\): normal (no action needed);
- \(s_{2}\): damaged (needs to be repaired);
- \(s_{3}\): destroyed (needs to be replaced);
- \(p_{s_{1}}(h, d)\) is equal to 1 the the flood duration and the water depth are negative or null and to 0 otherwise;
- \(p_{s_{2}}(h, d)\) is equal to 1 if the water depth is strictly positive and the flood duration positive and below 71 h and to 0 otherwise;
- \(p_{s_{3}}(h, d)\) is equal to 1 if the water depth is strictly positive and the flood duration is at least 71 h and to 0 otherwise;
- \(i_{s_{1}}(h, d)\), \(i_{s_{2}}(h, d)\), and \(i_{s_{3}}(h, d)\) are always equal to 1;
- \(c_{a_{s_{1}}}\) is equal to 0;
- \(c_{a_{s_{2}}}\) is equal to €22.5 by square meter that needs to be replaced;
- \(c_{a_{s_{3}}}\) is equal to €7365.5;
- \(h_{a_{s_{1}}}\) and \(h_{a_{s_{3}}}\) are equal to the height of the partition wall;
- \(h_{a_{s_{2}}}\) is equal to the height of the portion of the wall that was in contact with water.