Commented examples
Adaptation of elementary damage functions in model context
Simple example, one action, quantity fixed
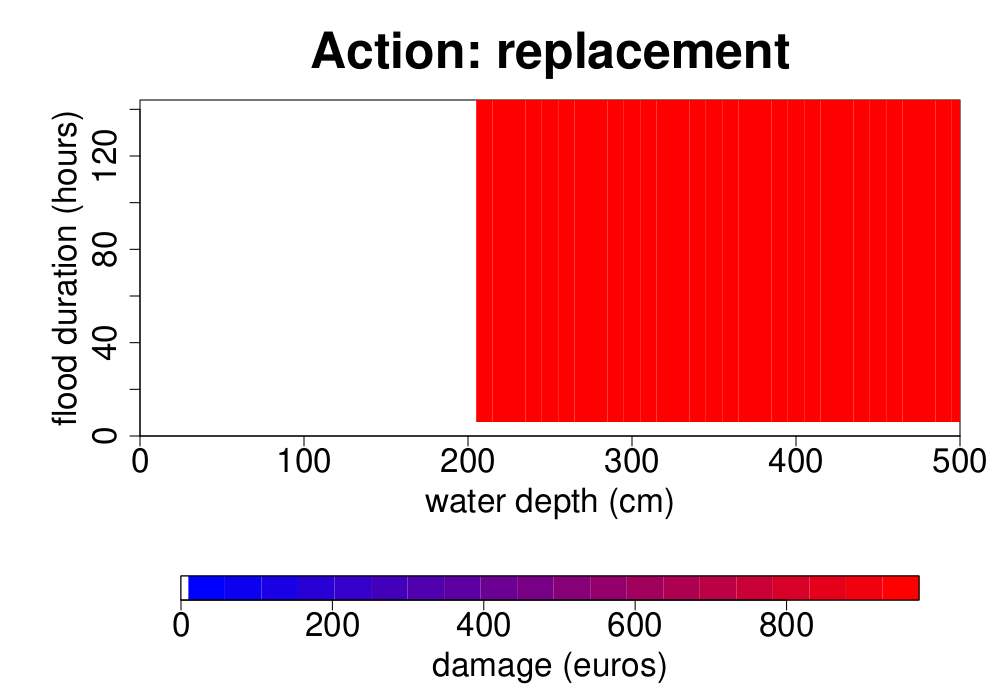
Figure Figure 1 shows the damage function of an air conditioner located in the model presented in the building model section. This damage function is different from the one of a decontextualized air conditioner presented in the elementary examples section in two aspects:
This air conditioner is located at 200 cm above the ground floor. Thus it needs to be replaced only from a water depth of 200 cm;
Moreover, it is associated to a dilapidation of 50%. Thus, its replacement value is half that of the decontextualized air conditioner, which is associated by default to a dilapidation of 0%.

Example, several actions, quantity fixed
Figure Figure 2 shows the damage function of a vending machine located in the model presented in the building model section. It differs from the damage function of the vending machine presented in the elementary examples section in the replacement value. Indeed, the new purchase value of the contextualized vending machine is given in the furniture file of the model. It is equal to €4 000, whereas the new purchase value taken into account to produce the decontextualized elementary damage function is equal to €3 000. This is due to the fact that the first value is the new purchase value of the specific vending machine considered, whereas the second is a default value, defined as the mean between the minimum and maximum new purchase values found in price catalogues or given by the experts. Moreover, the contextualized vending machine is associated to a dilapidation of 50%, whereas the decontextualized one has a dilapidation of 0%.
Example, complex actions
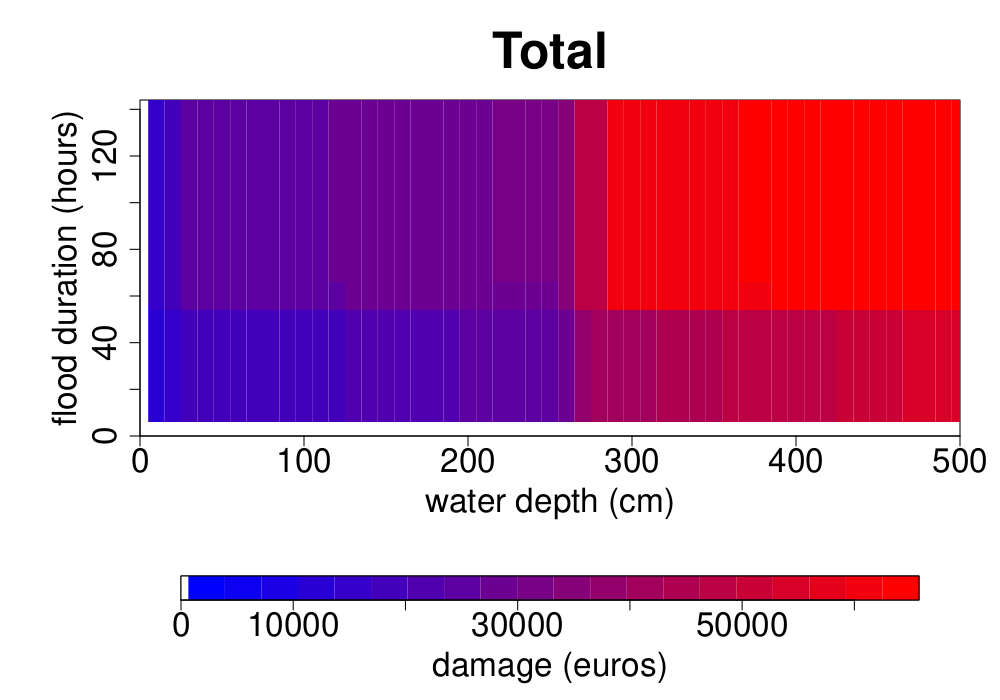
Figure Figure 3 shows the damage function of a gas-operated boiler located in the model presented in the building model section. Compared to the damage function of a decontextualized boiler, presented in the elementary examples section, it differs in two aspects:
the contextualized boiler is located 10 cm above the ground floor. Thus, the probability for it to be replaced is strictly positive only from a water depth of 10 cm;
it is associated to a dilapidation of 50%. Thus, its replacement value is half that of the decontextualized boiler.

Example, role of humidity
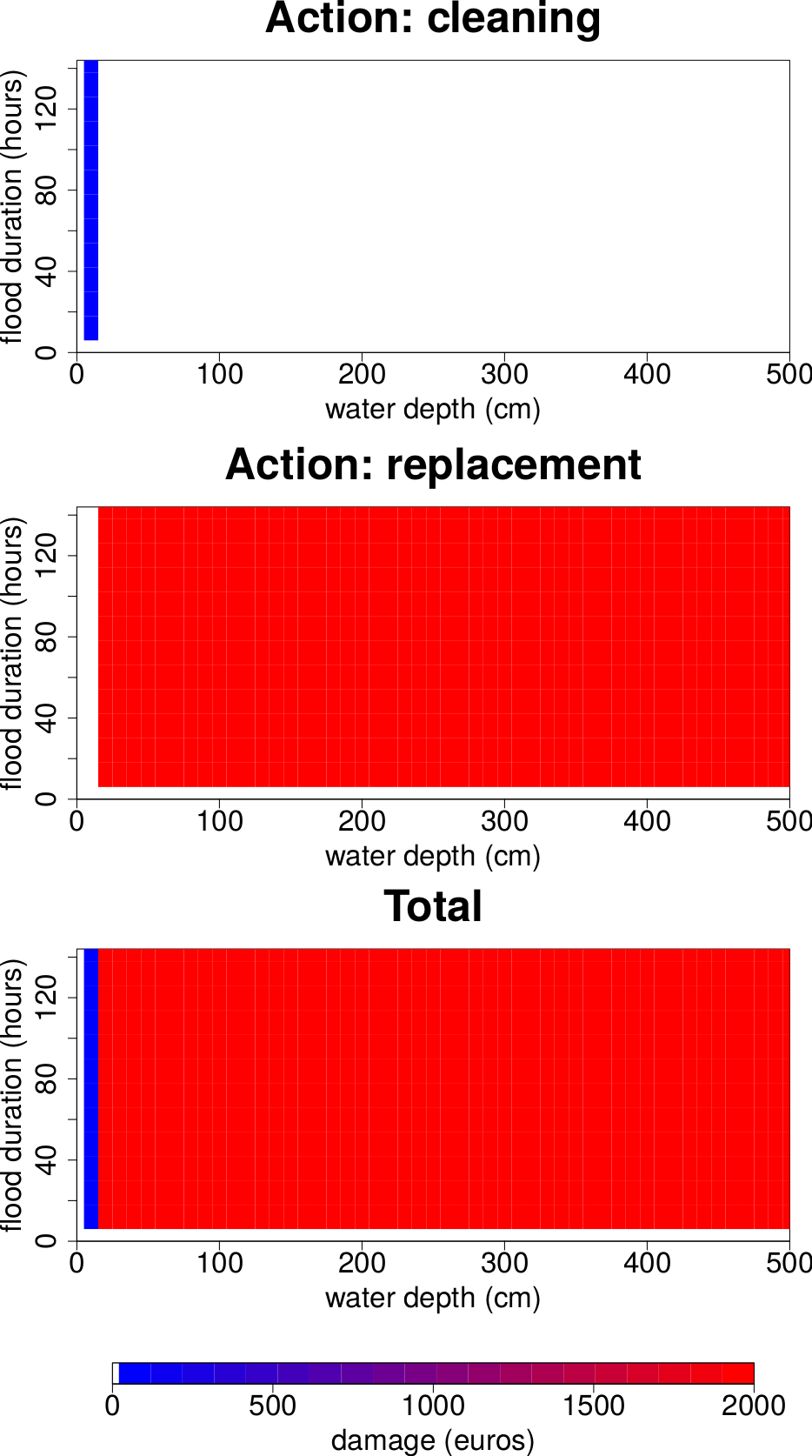
Figure Figure 4 shows the damage function of a computer located in the model presented in the building model section. It differs from the damage function of a decontextualized computer presented in the elementary examples section in 2 aspects:
since the computer is located at 100 cm above the ground floor, it needs to be dried for water depths comprised between 0 and 100 cm and it needs to be replaced for higher water depths;
the computer is associated to a dilapidation of 50%. Thus, its replacement value is half that of the decontextualized computer.

Example, quantity to be fixed
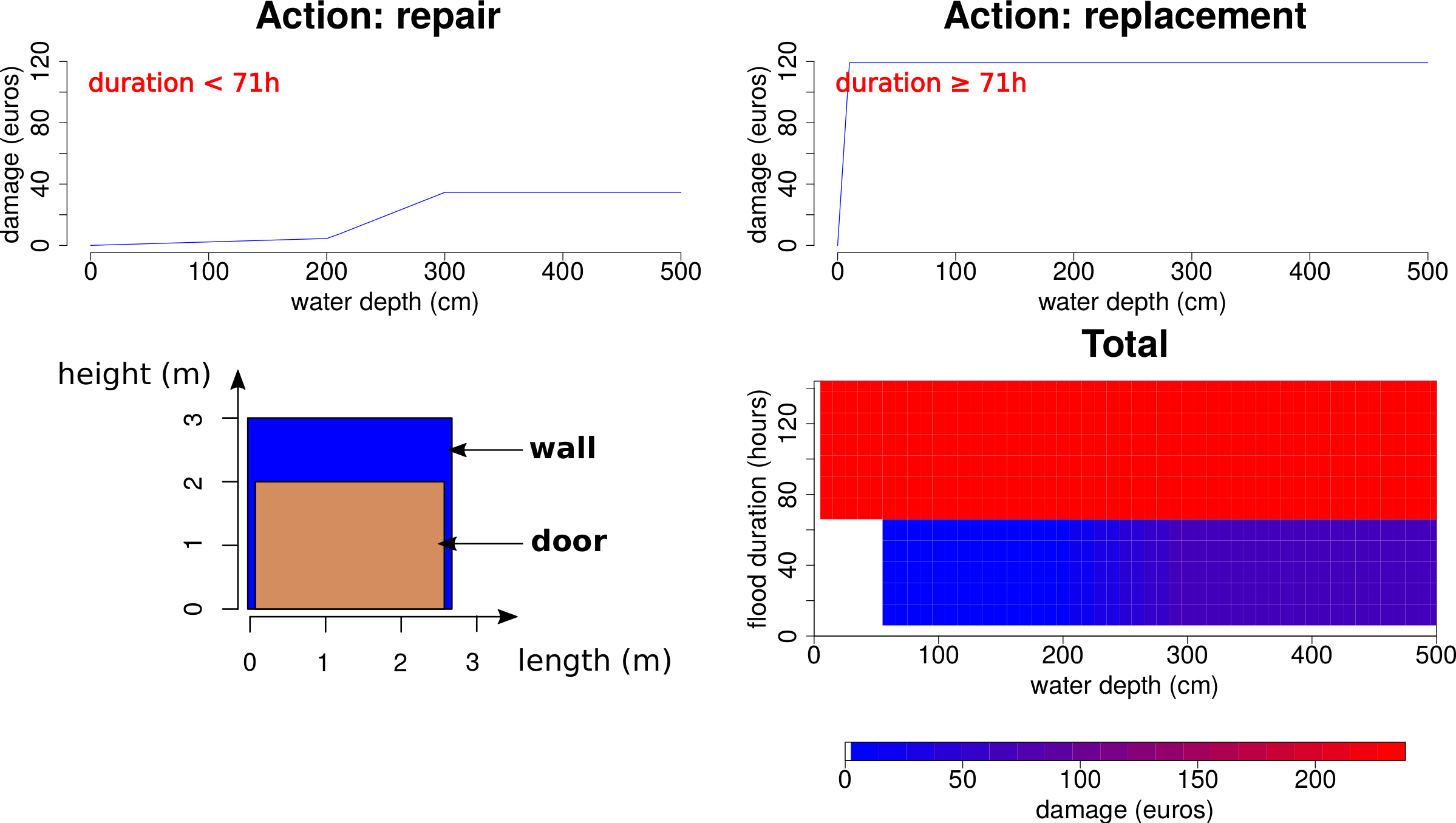
Figure Figure 5 shows the damage function of a wall in masonry located in the model presented in the building model section. This wall has a total length of 2.7 m and a height of 3 m. It supports a door with a width of 2.5 m and a height of 2 m. As a result, between 0 and 2 m from the floor, the portion of the wall made up of masonry is only 0.2 m. Thus, when it is affected by floods that last less than 71 h, the surface that needs to be repaired is equal to:
\(0.2~m * WaterDepth\) if the water depth is below 2 m;
\(0.2~m * 2~m + 2.7~m * (WaterDepth - 2~m)\) if the water depth is higher than 2 m.
When it is affected by floods that last at least 71 h, the replacement cost is equal to the replacement cost by square meter multiplied by the surface of the wall (\(0.2m * 2m + 2.7m * 1m = 3.1m^{2}\))
Single storey, uniform height
Figure Figure 6 shows the damage function of the single storey house represented in the building model section.

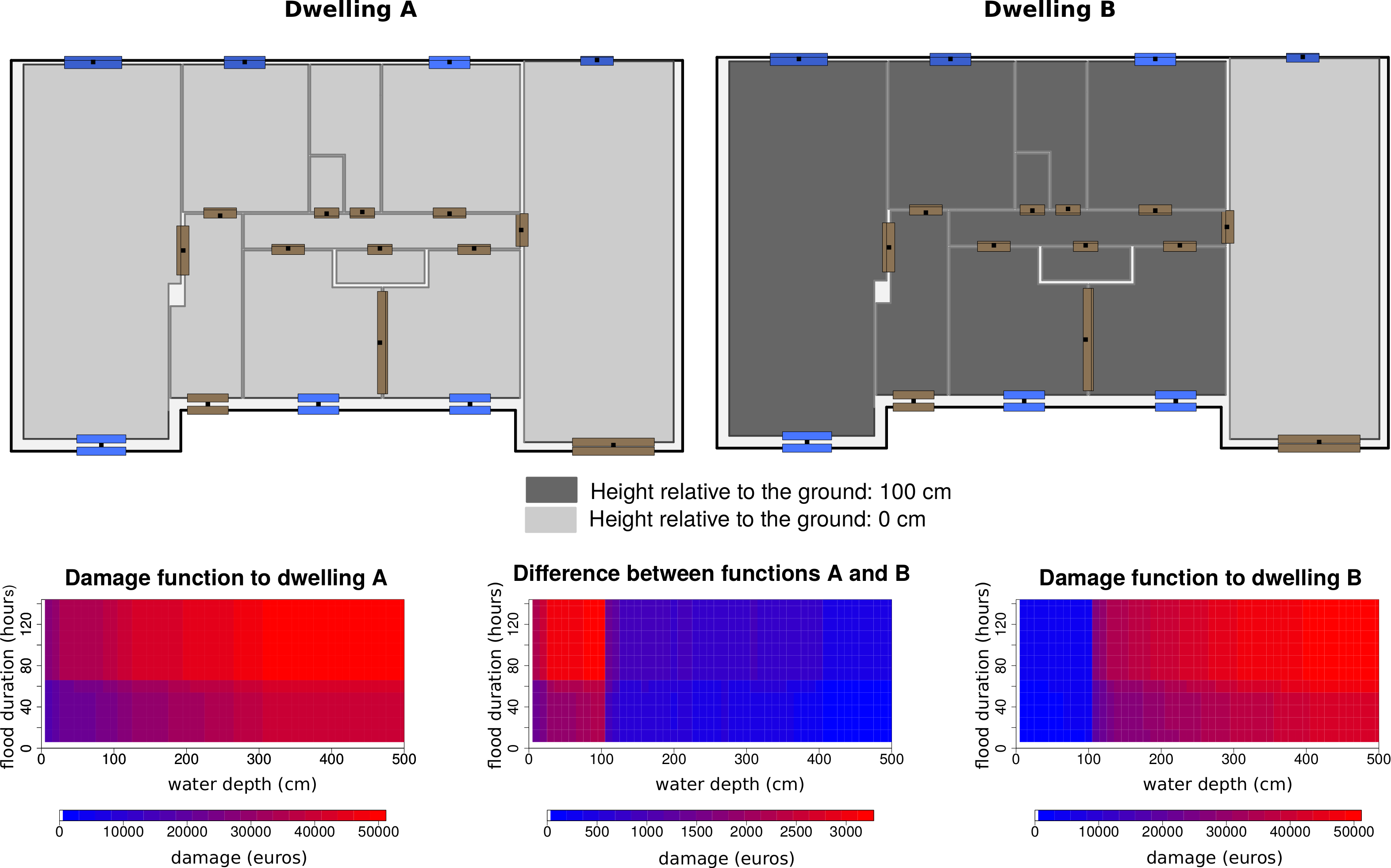
Single storey, different heights
Figure Figure 7 compares the damage function of the single storey house represented in the building model section, which is on the ground level, with the damage function of a similar house that has a varying elevation relative to the ground. The first damage function is always higher than the second one, but this difference decreases with the water depth.
Several storeys
Figure Figure 8 shows the damage function of a double storey house. Compared to the damage function of the single storey house (cf. figure Figure 6), the highest value of the damage is higher because the total surface of the double storey house is bigger. Moreover, we observe a threshold between the first and the second floor.